LA METHODE DES MOINDRES CARRES
La méthode des moindres carrés, indépendamment élaborée par Legendre et Gauss - figurant sur le billet de banque de 10 DM - au début du XIXe siècle, permet de comparer des données expérimentales, généralement entachées d’erreurs de mesure, à un modèle mathématique censé décrire ces données.
Ce modèle peut prendre diverses formes.
Il peut s’agir de lois de conservation que les quantités mesurées doivent respecter. La méthode des moindres carrés permet alors de minimiser l’impact des erreurs expérimentales en « ajoutant de l’information » dans le processus de mesure.
Le jour du Nouvel An de 1801, l'astronome italien Giuseppe Piazzi a découvert l'astéroïde Cérès. Il a alors pu suivre sa trajectoire jusqu'au 14 février 18012.
Durant cette année, plusieurs scientifiques ont tenté de prédire sa trajectoire sur la base des observations de Piazzi (à cette époque, la résolution des équations non linéaires de Kepler de la cinématique est un problème très difficile).
La plupart des prédictions furent erronées ; et le seul calcul suffisamment précis pour permettre à Zach, un astronome allemand, de localiser à nouveau Cérès à la fin de l'année, fut celui de Carl Friedrich Gauss, alors âgé de 24 ans (il avait déjà réalisé l'élaboration des concepts fondamentaux en 1795, lorsqu'il était alors âgé de 18 ans).
Mais sa méthode des moindres carrés ne fut publiée qu'en 1809, lorsqu'elle parut dans le tome 2 de ses travaux sur la mécanique céleste, Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium.
Le mathématicien français Adrien-Marie Legendre a développé indépendamment la même méthode en 1805. Le mathématicien américain Robert Adrain a publié en 1808 une formulation de la méthode.
En 1829, Gauss a pu donner les raisons de l'efficacité de cette méthode ; en effet, la méthode des moindres carrés est justement optimale à l'égard de bien des critères. Cet argument est maintenant connu sous le nom de théorème de Gauss-Markov.
Ce modèle peut prendre diverses formes.
Il peut s’agir de lois de conservation que les quantités mesurées doivent respecter. La méthode des moindres carrés permet alors de minimiser l’impact des erreurs expérimentales en « ajoutant de l’information » dans le processus de mesure.
Le jour du Nouvel An de 1801, l'astronome italien Giuseppe Piazzi a découvert l'astéroïde Cérès. Il a alors pu suivre sa trajectoire jusqu'au 14 février 18012.
Durant cette année, plusieurs scientifiques ont tenté de prédire sa trajectoire sur la base des observations de Piazzi (à cette époque, la résolution des équations non linéaires de Kepler de la cinématique est un problème très difficile).
La plupart des prédictions furent erronées ; et le seul calcul suffisamment précis pour permettre à Zach, un astronome allemand, de localiser à nouveau Cérès à la fin de l'année, fut celui de Carl Friedrich Gauss, alors âgé de 24 ans (il avait déjà réalisé l'élaboration des concepts fondamentaux en 1795, lorsqu'il était alors âgé de 18 ans).
Mais sa méthode des moindres carrés ne fut publiée qu'en 1809, lorsqu'elle parut dans le tome 2 de ses travaux sur la mécanique céleste, Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium.
Le mathématicien français Adrien-Marie Legendre a développé indépendamment la même méthode en 1805. Le mathématicien américain Robert Adrain a publié en 1808 une formulation de la méthode.
En 1829, Gauss a pu donner les raisons de l'efficacité de cette méthode ; en effet, la méthode des moindres carrés est justement optimale à l'égard de bien des critères. Cet argument est maintenant connu sous le nom de théorème de Gauss-Markov.
APPLICATION A LA GEODESIE, LA TOPOGRAPHIE, LA PHOTOGRAMMETRIE, LE GNSS ...
Le domaine d'application de la Méthode des Moindres Carrés est multiple et sans cette méthode nous ne pourrions certainement pas fixer un point avec le système de positionnement global GNSS !
Nous avons débuté dans la pratique des ajustements par la Méthode des Moindres Carrés lors de nos stages à la Direction des Grands Levers et Plans Généraux du Cadastre. A l'époque, il fallait remplir de grandes feuilles de papier avec les équations d'observations, la résolution des équations normales et le calcul des paramètres statistiques. Que ce soit pour un relèvement sur des points connus en coordonnées ou pour les réseaux de polygonales, l'application de la Méthode des Moindres Carrés nous fournissaient les coordonnées "ajustées". Déjà à époque, nous avions programmé sur des calculatrices HP des solutions basées sur cette méthode ainsi que sur les premier ordinateur portable.
C'est lors de notre passage à l'Institut Géographique National Belge, direction de la Géodésie, que nous avons vraiment développé les applications de la Méthode des Moindres Carrés à la fois pour le traitement des "runs" réalisés à l'aide de la plateforme inertielle FERRANTI II mais également pour les mises à jour du réseau géodésique. Nous avons également réalisé le logiciel d'ajustement des lignes de base GPS avec intégration dans le système de coordonnée LB 72. Avec les théories sur l'optimisation des réseaux géodésiques et la méthode de test du Professeur Baarda, nous avons développé davantage d'applications.
C'est chez STAR INFORMATIC que nous avons également intégré la Méthode des Moindres Carrés aux observations topographiques dans le logiciel STAR TOPO UX.
Depuis, nous avons continué à développer des applications qui font toujours largement appel à cette méthode. Les projets d'auscultation et de surveillance géodésique, les mesures industrielles ainsi que les développements en photogrammétrie numérique sont naturellement une terre d'élection pour cette méthode.
Nous avons donc acquis une expérience considérable dans ce moyen de traitement que nous partageons régulièrement par le biais de formation sur mesure.
Outre l'obtention des paramètres (coordonnées), la Méthode des Moindres Carrés permet en mode "simulation" ou "optimisation" de guider le design d'un réseau d'observation topographique et géodésique en garantissant au client que les précisions attendues seront respectées avec une instrumentation adaptée et non sur-dimensionnée.
Nous avons débuté dans la pratique des ajustements par la Méthode des Moindres Carrés lors de nos stages à la Direction des Grands Levers et Plans Généraux du Cadastre. A l'époque, il fallait remplir de grandes feuilles de papier avec les équations d'observations, la résolution des équations normales et le calcul des paramètres statistiques. Que ce soit pour un relèvement sur des points connus en coordonnées ou pour les réseaux de polygonales, l'application de la Méthode des Moindres Carrés nous fournissaient les coordonnées "ajustées". Déjà à époque, nous avions programmé sur des calculatrices HP des solutions basées sur cette méthode ainsi que sur les premier ordinateur portable.
C'est lors de notre passage à l'Institut Géographique National Belge, direction de la Géodésie, que nous avons vraiment développé les applications de la Méthode des Moindres Carrés à la fois pour le traitement des "runs" réalisés à l'aide de la plateforme inertielle FERRANTI II mais également pour les mises à jour du réseau géodésique. Nous avons également réalisé le logiciel d'ajustement des lignes de base GPS avec intégration dans le système de coordonnée LB 72. Avec les théories sur l'optimisation des réseaux géodésiques et la méthode de test du Professeur Baarda, nous avons développé davantage d'applications.
C'est chez STAR INFORMATIC que nous avons également intégré la Méthode des Moindres Carrés aux observations topographiques dans le logiciel STAR TOPO UX.
Depuis, nous avons continué à développer des applications qui font toujours largement appel à cette méthode. Les projets d'auscultation et de surveillance géodésique, les mesures industrielles ainsi que les développements en photogrammétrie numérique sont naturellement une terre d'élection pour cette méthode.
Nous avons donc acquis une expérience considérable dans ce moyen de traitement que nous partageons régulièrement par le biais de formation sur mesure.
Outre l'obtention des paramètres (coordonnées), la Méthode des Moindres Carrés permet en mode "simulation" ou "optimisation" de guider le design d'un réseau d'observation topographique et géodésique en garantissant au client que les précisions attendues seront respectées avec une instrumentation adaptée et non sur-dimensionnée.
LOGICIELS DISPONIBLES
Il existe actuellement plusieurs logiciels qui permettent de traiter les observations topographiques et géodésiques par la Méthode des Moindres Carrés et dont CGEOS a l'expertise.
Citons entre autres :
Ils se différentient généralement par les modèles statistiques et les informations relatives aux calculs.
Citons entre autres :
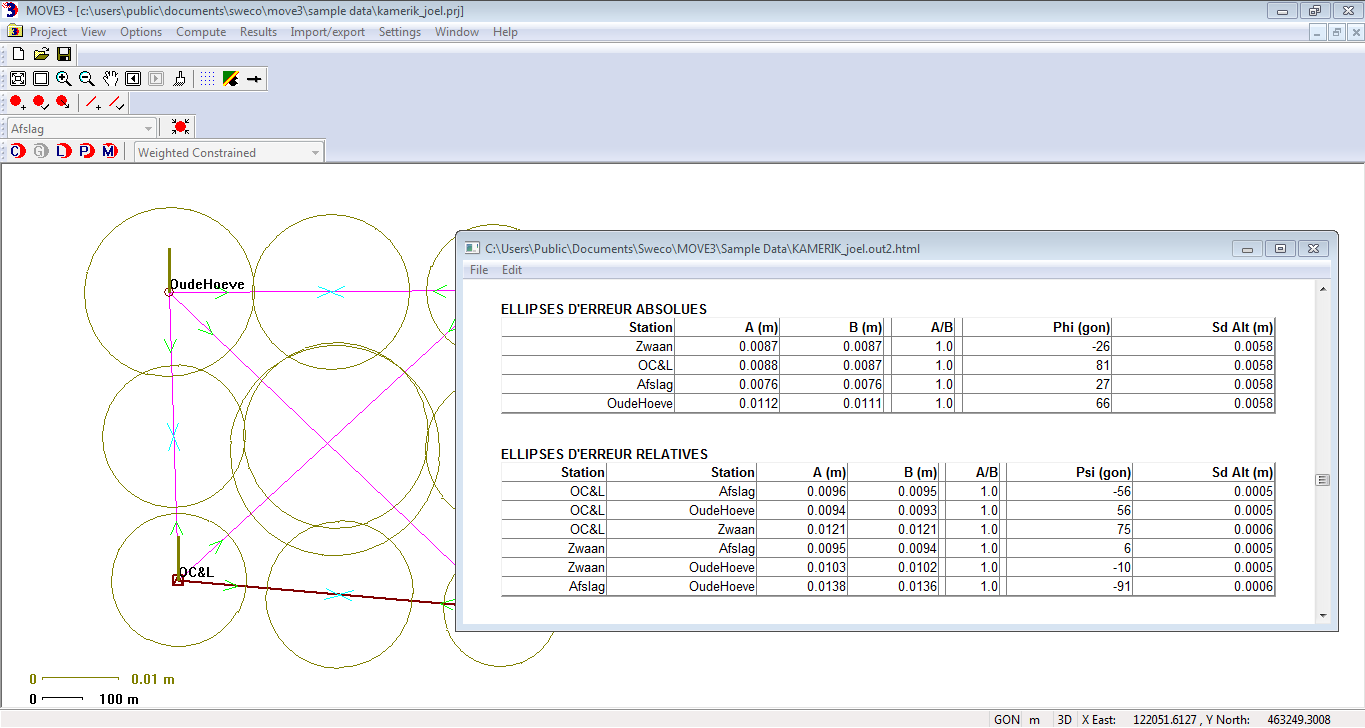
- MOVE 3D de Sweco Nederland B.V.
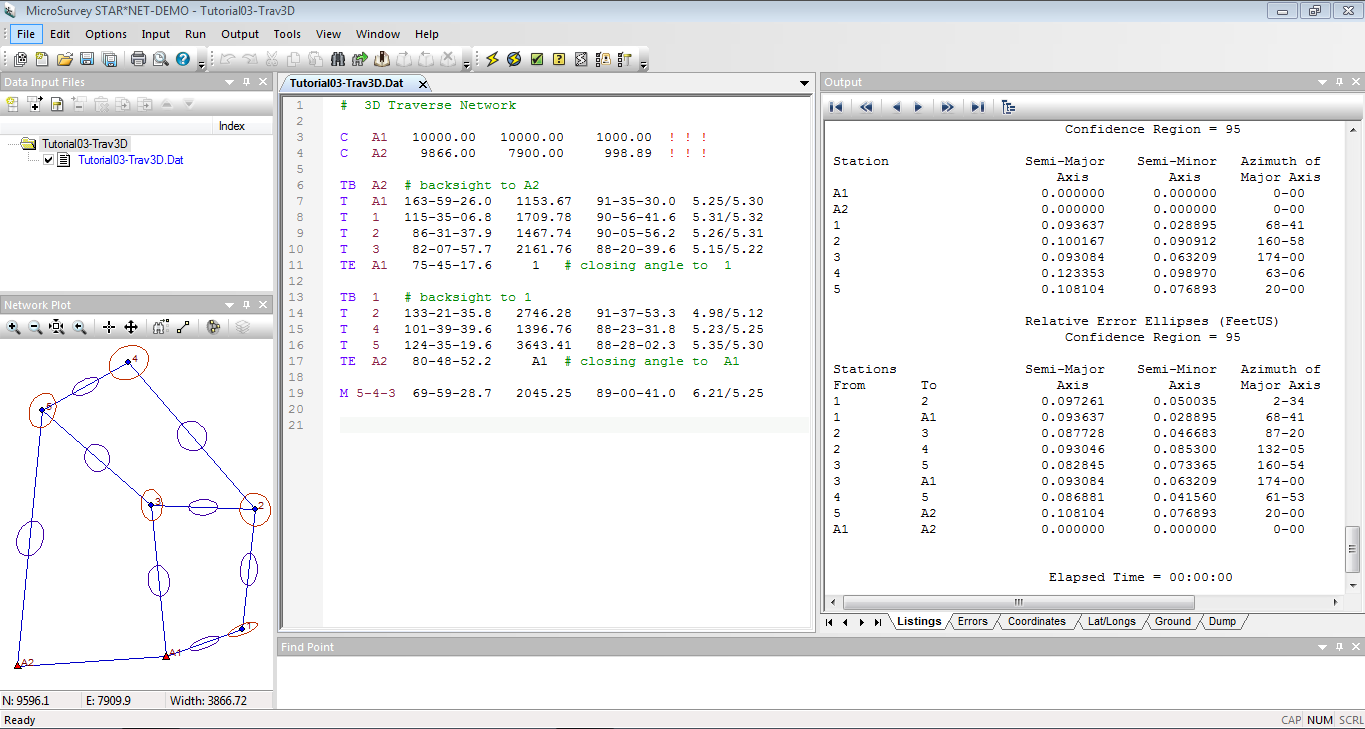
- STAR*NET de MicroSurvey Canada
- LisCad de la société LISTECH Australie
- etc, ...
Ils se différentient généralement par les modèles statistiques et les informations relatives aux calculs.
PROPOSITION DE CGEOS
De part notre expertise dans l'application de la Méthode des Moindres Carrés, nous somme à même de développer des applications sur mesure dans tous les domaines de la topographie, de la géodésie, des mesures industrielles et la photogrammétrie.
Nous pouvons également superviser et diriger la rédaction de spécifications techniques ayant trait à la description des précisions à garantir et les paramètres à délivrer ainsi que les tests de qualité.
Enfin, nous pouvons organiser des formations sur mesure pour les professionnels qui le désirent.
Nous pouvons également superviser et diriger la rédaction de spécifications techniques ayant trait à la description des précisions à garantir et les paramètres à délivrer ainsi que les tests de qualité.
Enfin, nous pouvons organiser des formations sur mesure pour les professionnels qui le désirent.
PRESENTATIONs
Nous avons réalisé de nombreuses présentations en PPTX sur la Méthode des Moindres Carrés, n'hésitez pas à nous contactez pour obtenir des copies ! Vous trouverez ici une copie d'une présentation de base que les étudiants peuvent exploiter dans le cours de Topométrie Avancée.
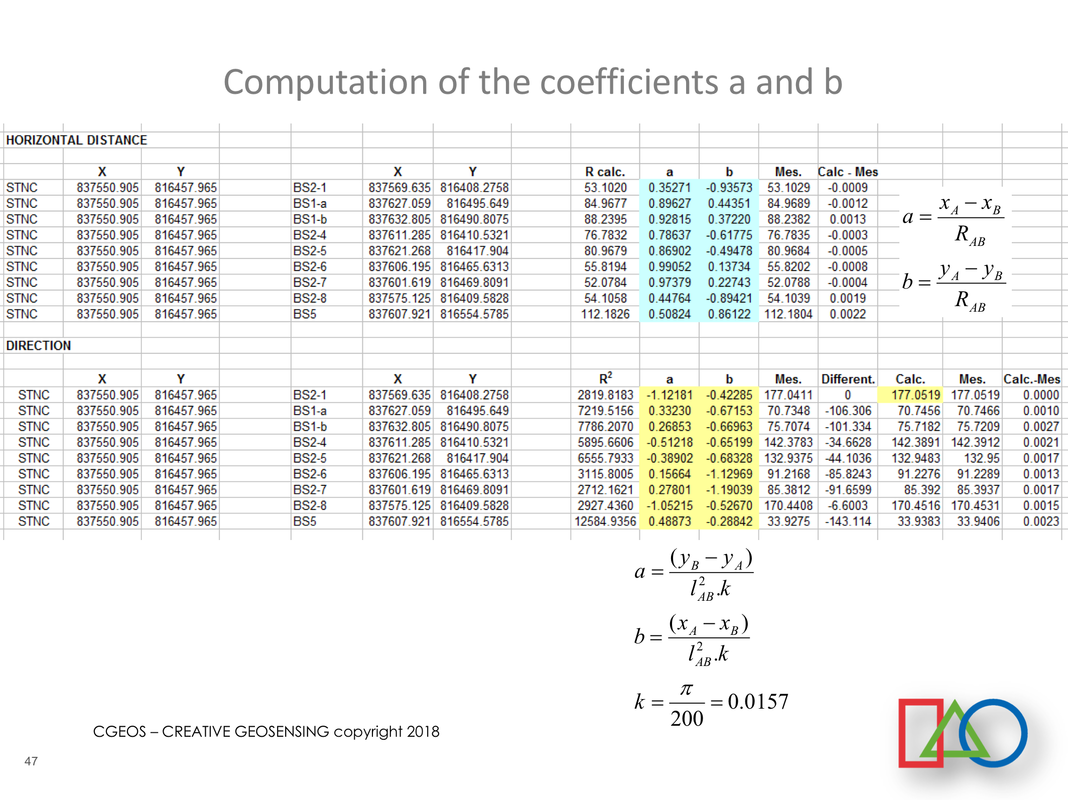
Certaines de nos présentations exposent toutes les équations d'observation (1D, 2D, 3D) et les différents modèles mathématiques utilisés ainsi qu'une présentation détaillée sur les tests statistiques incluant la méthode de test développée par le Professeur Baarda.
Il existe des problèmes en topographie qui n'ont de solution qu'à l'aide de cette méthode.
Certaines de nos présentations exposent toutes les équations d'observation (1D, 2D, 3D) et les différents modèles mathématiques utilisés ainsi qu'une présentation détaillée sur les tests statistiques incluant la méthode de test développée par le Professeur Baarda.
Il existe des problèmes en topographie qui n'ont de solution qu'à l'aide de cette méthode.
| leastsquaresadjustment_jvc_2018.pptx | |
| File Size: | 5760 kb |
| File Type: | pptx |